Summary

This article is a summary of my work in my final project of UC Berkeley’s CS 267 Applications of Parallel Computers. Our report can be accessed here. The main idea of the project is to speed up the training process of reinforcement learning (RL) by parallelizing the execution of environments. I implemented and tested a parallelized CartPole environment using PyTorch Tensor and another one using Numba kernels. I did the scaling tests of these two environments along with Stable Baselines’ vectorized environments.

Stable Baselines, RLlib, and Isaac Gym

Stable Baselines’ vectorized environment leverages Python’s multiprocessing library, which spawns worker processes. Each worker process executes one environment and sends the results to the main process, which introduces overhead from the inter-process communication. RLlib provides remote environments, which create env instances in Ray actors and step them in parallel. These remote processes introduce communication overheads and only help if the environment is very expensive to step / reset. NVIDIA has announced Isaac Gym, a physics simulation environment for reinforcement learning research. Isaac Gym enables a complete end-to-end GPU RL pipeline by leveraging NVIDIA’s PhysX GPU-accelerated simulation engine, which allows it to gather the experience data required for robotics RL. Isaac Gym also enables observation and reward calculations to take place on the GPU, thereby avoiding significant performance bottlenecks. In particular, costly data transfers between the GPU and the CPU are eliminated. NVIDIA declares that researchers can achieve the same level of success as OpenAI’s supercomputer on a single GPU in about 10 hours.

Stable Baselines’ Vectorized Environments

I used the Cartpole environment for testing. I first tested Stable Baselines’ vectorized environments, which uses a wrapper for multiple environments, calling each environment in sequence on the current Python process. In the experiment, the number of environments is bounded above by 32 on Google Colab, and the run time of an environment step increases almost linearly even when it is under 32, meaning that this approach could not improve throughput effectively.

Parallelism via PyTorch Tensor

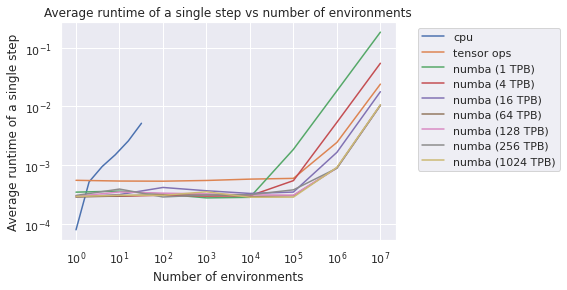
Inspired by this post, I rewrote CartPole-v1 using PyTorch Tensor operations. All the state vectors and calculations are performed on a CUDA GPU, which significantly speeds up the performance. However, the operations are executed sequentially, which means threads that finish earlier have to wait until other threads to finish.

import numpy as np
import torch
import math
from gym import spaces

class CartPole:
    metadata = {
        'render.modes': ['human', 'rgb_array'],
        'video.frames_per_second': 50
    }

    def __init__(self, env_count=1, device="cpu"):
        self.gravity = 9.8
        self.masscart = 1.0
        self.masspole = 0.1
        self.total_mass = (self.masspole + self.masscart)
        self.length = 0.5  # actually half the pole's length
        self.polemass_length = (self.masspole * self.length)
        self.force_mag = 10.0
        self.tau = 0.02  # seconds between state updates
        self.kinematics_integrator = 'euler'

        # Angle at which to fail the episode
        self.theta_threshold_radians = 12 * 2 * math.pi / 360
        self.x_threshold = 2.4
        self.env_count = env_count
        
        # Angle limit set to 2 * theta_threshold_radians so failing observation
        # is still within bounds.
        high = np.array([self.x_threshold * 2,
                         np.finfo(np.float32).max,
                         self.theta_threshold_radians * 2,
                         np.finfo(np.float32).max],
                        dtype=np.float32)

        self.action_space = spaces.Discrete(2)
        self.observation_space = spaces.Box(-high, high, dtype=np.float32)

        self.seed()
        self.viewer = None
        self.state = None
        self.done = torch.full([env_count], True, dtype=torch.bool, device=device)
        self.state = torch.zeros([self.env_count, 4], dtype=torch.float32, device=device)

        self.device = device

    def seed(self, seed=None):
        return [seed]

    def step(self, action, auto_reset=True):

        #breakpoint()
        # All env must already have been reset.
        self.done[:] = False
        x, x_dot, theta, theta_dot = self.state[:, 0], self.state[:, 1], self.state[:, 2], self.state[:, 3]
        #breakpoint()
        force = self.force_mag * ((action * 2.) - 1.)
        
        costheta = torch.cos(theta)
        sintheta = torch.sin(theta)

        # For the interested reader:
        # https://coneural.org/florian/papers/05_cart_pole.pdf
        temp = (force + self.polemass_length * theta_dot ** 2 * sintheta) / self.total_mass
        thetaacc = ((self.gravity * sintheta - costheta * temp) 
                    / (self.length * (4.0 / 3.0 - self.masspole * costheta ** 2 / self.total_mass)))
        xacc = temp - self.polemass_length * thetaacc * costheta / self.total_mass

        if self.kinematics_integrator == 'euler':
            x = x + self.tau * x_dot
            x_dot = x_dot + self.tau * xacc
            theta = theta + self.tau * theta_dot
            theta_dot = theta_dot + self.tau * thetaacc
        else:  # semi-implicit euler
            x_dot = x_dot + self.tau * xacc
            x = x + self.tau * x_dot
            theta_dot = theta_dot + self.tau * thetaacc
            theta = theta + self.tau * theta_dot

        self.state[:, 0], self.state[:, 1], self.state[:, 2], self.state[:, 3] = x, x_dot, theta, theta_dot

        self.done = (
            (x < -self.x_threshold)
            | (x > self.x_threshold)
            | (theta < -self.theta_threshold_radians)
            | (theta > self.theta_threshold_radians)
        )
        reward = ~self.done
        
        if auto_reset:
          self.state = self.reset()
        return self.state, reward, self.done, {}

    def reset(self):
        #breakpoint()
        self.state = torch.where(self.done.unsqueeze(1), (torch.rand(self.env_count, 4, device=self.device) -0.5) / 10., self.state) 
        #self.state = (torch.rand((self.env_count, 4)) -0.5) / 10.
        return self.state

Parallelism via Numba Kernels

Numba’s CUDA Kernel provides a convenient interface to use GPU in a Python program. This approach gives the best performance among the three approaches. There is one hyperparameter I need to specify: the number of threads per block (TPB), because the number of thread blocks could be calculated given tensor size and TPB). I tested the run time of a single environment step with different TPBs and found that 64 and above give the best performance.

import numpy as np
from numba import cuda
import math
from gym import spaces

rng_limit = int(1e7)

@cuda.jit
def reset_kernel(state, rng_states):
    i = cuda.grid(1)
    if i < state.shape[0]:
      state[i,0]=(cuda.random.xoroshiro128p_uniform_float32(rng_states,i%rng_limit) -0.5) / 10.
      state[i,1]=(cuda.random.xoroshiro128p_uniform_float32(rng_states,i%rng_limit) -0.5) / 10.
      state[i,2]=(cuda.random.xoroshiro128p_uniform_float32(rng_states,i%rng_limit) -0.5) / 10.
      state[i,3]=(cuda.random.xoroshiro128p_uniform_float32(rng_states,i%rng_limit) -0.5) / 10.

@cuda.jit
def step_kernel(state, action, done, reward, rng_states):
    gravity = 9.8
    masscart = 1.0
    masspole = 0.1
    total_mass = (masspole + masscart)
    length = 0.5  # actually half the pole's length
    polemass_length = (masspole * length)
    force_mag = 10.0
    tau = 0.02  # seconds between state updates
    kinematics_integrator = 'euler'

    # Angle at which to fail the episode
    theta_threshold_radians = 12 * 2 * math.pi / 360
    x_threshold = 2.4
    i = cuda.grid(1)
    if i < state.shape[0]:
      #breakpoint()
      # All env must already have been reset.
      done[i] = False
      x, x_dot, theta, theta_dot = state[i, 0], state[i, 1], state[i, 2], state[i, 3]
      #breakpoint()
      force = force_mag * ((action[i] * 2.) - 1.)
      
      costheta = math.cos(theta)
      sintheta = math.sin(theta)

      # For the interested reader:
      # https://coneural.org/florian/papers/05_cart_pole.pdf
      temp = (force + polemass_length * theta_dot ** 2 * sintheta) / total_mass
      thetaacc = ((gravity * sintheta - costheta * temp) 
                  / (length * (4.0 / 3.0 - masspole * costheta ** 2 / total_mass)))
      xacc = temp - polemass_length * thetaacc * costheta / total_mass

      if kinematics_integrator == 'euler':
          x = x + tau * x_dot
          x_dot = x_dot + tau * xacc
          theta = theta + tau * theta_dot
          theta_dot = theta_dot + tau * thetaacc
      else:  # semi-implicit euler
          x_dot = x_dot + tau * xacc
          x = x + tau * x_dot
          theta_dot = theta_dot + tau * thetaacc
          theta = theta + tau * theta_dot

      state[i, 0], state[i, 1], state[i, 2], state[i, 3] = x, x_dot, theta, theta_dot

      done[i] = (
          (x < -x_threshold)
          | (x > x_threshold)
          | (theta < -theta_threshold_radians)
          | (theta > theta_threshold_radians)
      )
      reward[i] = ~done[i]
      
      if done[i]:
       state[i,0]=(cuda.random.xoroshiro128p_uniform_float32(rng_states,i%rng_limit) -0.5) / 10.
       state[i,1]=(cuda.random.xoroshiro128p_uniform_float32(rng_states,i%rng_limit) -0.5) / 10.
       state[i,2]=(cuda.random.xoroshiro128p_uniform_float32(rng_states,i%rng_limit) -0.5) / 10.
       state[i,3]=(cuda.random.xoroshiro128p_uniform_float32(rng_states,i%rng_limit) -0.5) / 10.

class CartPole2:
    metadata = {
        'render.modes': ['human', 'rgb_array'],
        'video.frames_per_second': 50
    }

    def __init__(self, env_count=1, tpb=1):
        self.gravity = 9.8
        self.masscart = 1.0
        self.masspole = 0.1
        self.total_mass = (self.masspole + self.masscart)
        self.length = 0.5  # actually half the pole's length
        self.polemass_length = (self.masspole * self.length)
        self.force_mag = 10.0
        self.tau = 0.02  # seconds between state updates
        self.kinematics_integrator = 'euler'

        # Angle at which to fail the episode
        self.theta_threshold_radians = 12 * 2 * math.pi / 360
        self.x_threshold = 2.4
        self.env_count = env_count
        
        # Angle limit set to 2 * theta_threshold_radians so failing observation
        # is still within bounds.
        high = np.array([self.x_threshold * 2,
                         np.finfo(np.float32).max,
                         self.theta_threshold_radians * 2,
                         np.finfo(np.float32).max],
                        dtype=np.float32)

        self.action_space = spaces.Discrete(2)
        self.observation_space = spaces.Box(-high, high, dtype=np.float32)

        self.seed()
        self.viewer = None
        self.state = None
        self.done = cuda.to_device(np.full([env_count], True, dtype=np.bool))
        self.state = cuda.device_array([self.env_count, 4], dtype=np.float32)
        self.reward=cuda.to_device(np.zeros((env_count,)))
        self.rng_states = cuda.random.create_xoroshiro128p_states(min(env_count,rng_limit), seed=0)
        self.env_count=env_count
        self.num_envs=env_count
        self.tpb=tpb

    def seed(self, seed=None):
        return [seed]

    def step(self, action, copy=True):
        step_kernel[math.ceil(self.env_count/self.tpb), self.tpb](self.state, action, self.done, self.reward, self.rng_states)
        return self.state, self.reward, self.done.copy_to_host() if copy else self.done, {}
    
    def reset(self):
        reset_kernel[math.ceil(self.env_count/self.tpb), self.tpb](self.state, self.rng_states)
        return self.state

Impact on Training Process

Another student in our project team tested the environments on an on-policy RL algorithm, PPO. The results showed that although more parallelization gives more samples, it does not necessarily improve the training rewards. One possible reason is that the learner processed all the transitions in one batch. One way to avoid this is to use a distributed RL algorithm like R2D2.

Conclusion

Using CUDA could improve the throughput of reinforcement learning by speeding up the environment steps. The next step is to test its impact on training time and rewards for different RL algorithms.